Quantino-Theorie
Erste Seite | « | 1 ... 6 | 7 | 8 | 9 | » | Letzte
[ Nach unten | Zum letzten Beitrag | Thema abonnieren | Neueste Beiträge zuerst ]
Re: Quantino-Theorie
von Steffen am 09.05.2016 21:25Hallo Lothar,
Ich bin davon ausgegangen, bzw. habe es so postuliert, dass Quantinos keine räumliche Ausdehnung haben. Sie sind also - im Modell - perfekt punktförmig. Die Wechselwirkung erfolgt dann und nur dann, wenn sich das Quantino lange genug in einer (Einheits-)ladung aufhällt. Eine Einheitsladung hat ein bestimmtes universelles Volumen. Aus dem universellen Volumen und der universellen Minimalwechselwirkungszeit folgt im Übrigen die universelle Konstanz der Lichtgeschwindigkeit.
Lies Dir mal bitte ganz genau die Postulate durch. Also Wort für Wort. Es sollte in sich vollständig sein. Es ist aber ein Modell, das darf man nicht vergessen. Genau wie die newtonschen Axiome oder die Maxwellgleichungen nur ein Modell sind.
Kann ich machen.
Grüße
Steffen
Re: Quantino-Theorie
von Struktron am 09.05.2016 22:52Hallo Steffen,
die Links zu den mathematischen Definitionen sollen also noch kommen.
Für die Quantinos, welche im Vakuum nicht wechselwirken sollen, muss die Auswahl eines konkreten Geschwindigkeitswertes demnach in den Ladungen erfolgen. Das kann ein Zufallsgenerator erledigen. Dessen MB-Verteilung ergibt sich möglicherweise durch eine Mastergleichung für die Ladung. Viel darüber steht in Haken, Hermann; Synergetik. Eine Einführung. Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie, Springer-Verlag 1983 (Übersetzung Arne Wunderlin von: Synergetics. An Introduction.)
Gilt reine Superposition, bleiben die einmal erzeugten (von Anbeginn an vorgegebenen) Geschwindigkeiten erhalten. Die Ladungsbewegung kann dann als Schwerpunktsbewegung aufgefasst werden. Bei einer gedanklichen Trennung zwischen größeren und kleineren Geschwindigkeiten als c, kann daraus ein Druck oder Sog entstehen.
Mal sehen, was dabei noch heraus kommt.
MfG
Lothar W.
Re: Quantino-Theorie
von Steffen am 10.05.2016 21:57Hallo Lothar,
Unterhalb des Banners findest Du jetzt einen Link.
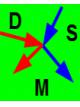
Dass es eine Maxwell-Boltzmann-Verteilung ist, ist nur eine Vermutung von mir. Experimentelle Untersuchungen dazu gibt es ja nicht. Abbildung 1.1.1.3 zeigt schraffiert den Bereich, der für die Maxwellgleichungen relevant ist. Alles andere ist völliges Neuland für die Physik. Nicht mal die Experimente am CERN können da in irgend einer Weise weiterhelfen, da sie mit ihrem stationären Beschleuniger - so groß er auch sein mag - grundsätzlich nichts auf Überlichtgeschwindigkeit beschleunigen können.
Aber wenn es wirklich eine Maxwell-Boltzmann-Verteilung sein sollte, heißt das, dass die Ladungen in ihrem Innern sehr viele Quantinos enthalten, die eine Art ideales Gas bilden. Die Quantinos, die eine Einheitsladung verlassen, sind wahrscheinlich extreme Ausnahmen. Eine Art Zerfall quasi. Quantinos könnten auch durchaus miteinander wechselwirken, oder absorbiert werden. Das spielt aber keine Rolle, wenn ihre Dichte außerhalb von Ladungen nur gering genug ist.
Da ich mich für die Physik oberhalb dieses Levels interessiere, stört mich das alles nicht und nehme an, was am einfachsten ist und sich am besten rechnen lässt. Es ist eben nur ein Modell.
Genau.
Hier verstehe ich nicht, was Du meinst.
Viele Grüße
Steffen
Re: Quantino-Theorie
von Struktron am 11.05.2016 12:22Hallo Steffen,
Ja, den habe ich gesehen. Das fand ich aber auch bisher schon. Es fehlt mir z.B. bei jeder einzelnen Seite ein individueller Link auf den betreffenden Abschnitt Nehmen wir den Abschnitt 2.5 Die Relativität der Kraft. Da kommen wir, wenn wir auf Berechnungen kliicken, nicht auf die dazu gehörenden Berechnungen.
Fürs ideale Gas, bei welchem es keine Wechselwirkung zwischen den Partikeln gibt, kann das nur ein Postulat sein.
Problem ist bei jeder MB-Verteilung der kleine Bereich > c.
Da Du keine Wechselwirkung definierst, bleibt nur die Bewegung der Quantinos. Die Ermittlung der Durchschnittsgeschwindigkeit ist aber möglich. Daraus ergibt sich auch die durchschnittliche Bewegung des Ensembles. Kommt ein Quantino mit höherer Geschwindigkeit in die Ladung, wird deren Geschwindigkeit größer. Das kann man mit einem auf das gesamte Ensemble ausgeübtem Druck umschreiben. Kommt eines mit niedrigerer Geschwindigkeit ins Ensemble, fehlt in der durchschnittlichen Bewegungsrichtung etwas, diese (diie im Durchschnitt auch ruhen kann) erhält eine Geschwindigkeitsverringerung in der Herkunftsrichtung, was man dann als Sog umschreiben könnte.
Du musst allerdings noch etwas zum Unterschied der zwei Quantinoarten definieren, wenn sie nicht nur durch < oder > als c unterschieden werden.
MfG
Lothar W.
Re: Quantino-Theorie
von Steffen am 11.05.2016 20:57Hallo Lothar,
Die Links sind im Text verteilt. In dem Fall zum Beispiel im letzten Satz der Seite. Nicht zu jedem Text gibt es eine Berechnung oder wäre eine nötig. Mathematisch ist die Marschrichtung nämlich anders und man muss alles am Stück lesen. Wichtig ist hier vor allem die Herleitung des Quantinodrucks.
Ich verstehe jetzt, was Du meinst. Aber es wird im Fall der Quantinotheorie so nicht zu erklären gehen.
Eine Wechselwirkung ist aber schon definiert: Tritt ein Quantino in den Bereich einer Einheitsladung, und bleibt es dort für eine bestimmte Zeit, so kommt es zu einer Wechselwirkung (Regel 4). Was eine Wechselwirkung ist, wird in Regel 1 gesagt und durch Regel 3 konkretisiert. Die Regeln reichen aus, um damit eindeutig definierte Berechnungen auszuführen. Mehr ist für ein Modell auch nicht nötig und letztlich hat jedes Modell Postulate. Die Postulate der Elektrodynamik sind die Maxwellgleichungen. Experimente zeigen, dass sie gut sind. Die Quantinotheorie erklärt wiederum die Maxwellgleichungen, die drei Grundkräfte der klassichen Physik, die SRT, die newtonsche Mechanik und die Quantenmechanik. Also sind es ebenfalls gute Postulate. Vor allem sind sie weit weniger abstrakt, was ein Fortschritt für anschaulich denkende Menschen ist.
Aber die Quantinotheorie wird sich wie jede andere Theorie auch weiterentwickeln oder irgendwann durch etwas Besseres ersetzt werden. Ich rechne auch fest damit, dass für die Kernphysik Anpassungen nötig sein werden. Aber das ist nicht meine Baustelle.
Aus informationstechnischer und mathematischer Sicht nicht. Die Quantinoarten unterscheiden sich auch nicht durch kleiner oder größer c, sondern dadurch, dass negative Quantinos an positiven Einheitsladungen eine Geschwindigkeitsänderung entgegen der Bewegungsrichtung des Quantinos bewirken. Positive Quantinos bewirken an positiven Einheitsladungen eine Geschwindigkeitsänderung mit der Bewegungsrichtung (Regel 1). Das würde auch für Quantinos gelten, die Überlichtgeschwindigkeit in Bezug auf eine Ladung haben. Solche Quantinos kommen nur schon wieder aus der Einheitsladung heraus, bevor es zu einer Wechselwirkung gekommen ist (Regel 4). Sie sind damit wirkungslos, aber in keiner Weise anders.
Viele Grüße
Steffen
Re: Quantino-Theorie
von Struktron am 11.05.2016 23:32Hallo Steffen,
Deine dezent eingearbeiteten Links habe ich erst jetzt bemerkt, weil die meisten im Textteil auf Abbildungen verweisen. Im mathematischen Teil ist es so wohl ausreichend.
Zur Grundwechselwirkung muss ich noch etwas mehr nachdenken. Vorerst stelle ich mir die Frage, ob die Quantinos, wenn sie keine Audehnung besitzen, überhaupt wechselwirken können. Ein Feld um sie herum müsste eine Verteilungsfunktion besitzen, welche sich mit anderen überlagert (superponiert) und dann ab einer gewissen Stärke im deterministischen Fall die Wirkung auslöst. Ist für die Umgebung von vornherein eine Wahrscheinlichkeitsfunktion postuliert, stellt sich wiederum die Frage nach einer Erklärung.
Deine ganze Idee erinnert mich etwas an Weizsäckers Ure. Hast Du sein Buch: "Aufbau der Physik" gelesen?
MfG
Lothar W.
Re: Quantino-Theorie
von Steffen am 12.05.2016 21:47Hallo Lothar,
Wenn man ein Feld um die Quantinos herum postuliert, muss man auch beantworten, aus was dieses Feld besteht.
So wie die Posulate jetzt sind, ist es zumindest mathematisch klar: Wenn ein punktförmiges Quantino lange genug in einer Ladung war, kommt es zur Wechselwirkung. Wenn nicht, dann nicht. Ist eben beinahe Informatik.
Kenne ich leider nicht. Ich habe mich im letzten Jahr aber mal mit Ludwig Boltzmanns Werk auseinandergesetzt, weil dessen Arbeit mich irgendwie an Deine erinnert hat.
Viele Grüße
Steffen
Re: Quantino-Theorie
von Struktron am 12.05.2016 23:55Hallo Steffen,
Das bedeutet dann, dass langsamere stärker Wechselwirken.
Könnte das bei den zwei Quaninoarten entgegengesetzt sein? Wie wäre das dann zu erklären, als "Anti-Geschwindigkeit"?
Die Ure von Weizsäcker sind eigentlich Uralternativen. In seinem Buch schreibt er etwas davon. Online habe ich das Buch nicht kostenlos gefunden, habees aber in meinem Regal. Über Google findet man einiges, auch Quantentheorie der Uralternativen .
Boltzmanns Buch habe ich auch gelesen und ich bin ein echter Fan von ihm. Vielleicht zerbrach er sogar an der neuen Physik am Anfang des letzten Jarhunderts.
Momentan lese ich Heisenbergs "Der Teil und das Ganze". Daraus werden viele Zusammenhänge, auch über die Freundschaften,... verständlich. Er versuchte sich an einer einhetlichen Feldtheorie, die ich ebenfalls im Regal habe.
MfG
Lothar W.
Re: Quantino-Theorie
von Steffen am 13.05.2016 23:37Hallo Lothar,
Die Stärke der Wechselwirkung muss aus irgendeinem mir nicht bekannten Grund quadratisch zur Relativgeschwindigkeit sein. Wäre es anders, bekäme man nicht die Maxwellgleichungen. Ist Regel 3. Das passt auch zur Formel der kinetischen Energie, die auch quadratisch zur Relativgeschwindigkeit ist.
Dass was bei Wikipedia steht klingt eher abschreckend. Die Quantentheorie habe ich zu Anfang nicht berücksichtigt, bis mir auffiel, wie gut sich vieles damit erklären lässt.
Boltzmanns Arbeit ist beeindruckend. Er war ein echter Querdenker. Während alle in seiner Zeit mit Differentialgleichungen gearbeitet haben, hat er sich mit diskreter Statistik und Stochastik befasst. Er hat im Übrigen Planck zu seiner Arbeit über schwarze Körper inspiriert. Liest man diese Arbeit hört man förmlich Boltzmann.
Viele Grüße
Steffen
Re: Quantino-Theorie
von Struktron am 14.05.2016 15:34Hallo Steffen,
Du führst in 6.3.1 eine Proprtionalitätskonstante m_pho ein, wagst aber nicht den Schritt, das als Masse des Quantinos zu bezeichnen. Sie wird in kg ausgedrückt und es fehlt nur die numerische Größe, welche Du bisher nicht kennen kannst. Kinetische Energien sind in der klassischen Physik mit Impulsen verbunden und beide mit einer Wirkung verknüpft. Damit sollte sich ein elementares Wirkungsquantum ergeben, aber vermutliich nur im Durchschnitt vieler Quantinos.
Insgesamt sehe ich Deine Idee stark abhängig von den elementaren Wechselwirkungen und es fehlt mMn eine Aussage, ob Du alles aus diskreten Objekten aufgebaut betrachtest (auch Elementarteilchen, Moleküle,...) oder doch den Feldbegriff als wesentlich dafür erachtest (Superposition,...)?
Außerdem fiel mir auf, dass Du an verschiedenen Stellen von "Ringen" schreibst, wo Du eigentlich dreidimensionale Ausbreitung meinst, die als "Sphären" bezeichnet werden könnten.
MfG
Lothar W.

 Antworten
Antworten